A bond is a type of financial asset that represents a loan made by an investor to a borrower, typically a company or a government. When an investor buys a bond, they are essentially lending money to the borrower in exchange for regular coupon payments and a promise to repay the initial amount (nominal) at a future date, known as the bond's maturity date.
Bonds come in different types and are typically issued with a fixed coupon rate, which is determined at the time of issuance. The coupon payments are usually made periodically, such as monthly or annually, and the amount paid is determined by the coupon rate and the nominal.
Bonds are often considered a relatively safe investment because they are backed by the borrower's ability to repay the loan, and they offer a fixed rate of return. However, the value of bonds can also fluctuate based on changes in interest rates and market conditions.
In this post, we will build a model for a 10-year bond with an annual coupon. We will calculate the present value of future cash flows 6 months after the issue date. For this purpose, we will use the cashflower package, which is an open-source Python package for actuarial modelling.
List of content:
Cash flows profile
The cash flows profile of a bond from the perspective of an investor:
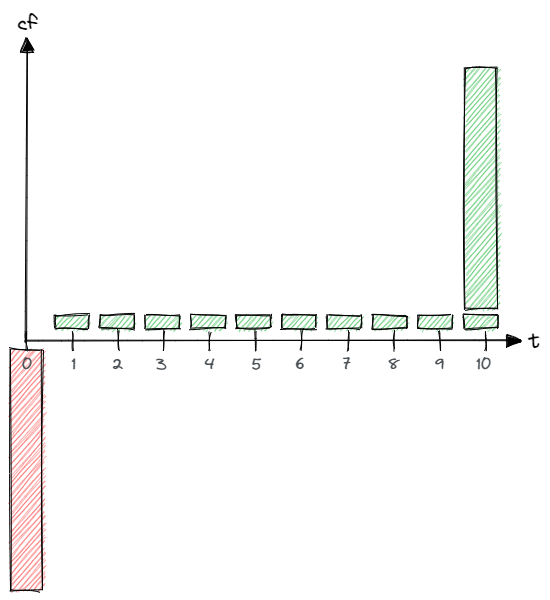
At the beginning, the investor pays nominal value to the borrower. The borrower pays coupons to the investor for 10 consecutive years. At the end of the term, the borrower returns the nominal to the investor.
Solution
We will firstly present the full solution and afterwards discuss each component in more details.
Input:
input.pyimport pandas as pd
from cashflower import Runplan, ModelPointSet
runplan = Runplan(data=pd.DataFrame({
"version": [1],
"valuation_year": [2022],
"valuation_month": [12],
}))
main = ModelPointSet(data=pd.DataFrame({
"id": [1],
"nominal": [1000],
"coupon_rate": [0.03],
"term": [120],
"issue_year": [2022],
"issue_month": [6],
}))
assumption = dict()
assumption["INTEREST_RATE"] = 0.02
Formulas:
model.pyfrom cashflower import variable
from input import main, runplan, assumption
from settings import settings
@variable()
def t_end():
years = main.get("term") // 12
months = main.get("term") - years * 12
end_year = main.get("issue_year") + years
end_month = main.get("issue_month") + months
if end_month > 12:
end_year += 1
end_month -= 12
valuation_year = runplan.get("valuation_year")
valuation_month = runplan.get("valuation_month")
return (end_year - valuation_year) * 12 + (end_month - valuation_month)
@variable()
def cal_month(t):
if t == 0:
return runplan.get("valuation_month")
if cal_month(t-1) == 12:
return 1
else:
return cal_month(t-1) + 1
@variable()
def cal_year(t):
if t == 0:
return runplan.get("valuation_year")
if cal_month(t-1) == 12:
return cal_year(t-1) + 1
else:
return cal_year(t-1)
@variable()
def coupon(t):
if t != 0 and t <= t_end() and cal_month(t) == main.get("issue_month"):
return main.get("nominal") * main.get("coupon_rate")
else:
return 0
@variable()
def nominal_value(t):
if t == t_end():
return main.get("nominal")
else:
return 0
@variable()
def present_value(t):
i = assumption["INTEREST_RATE"]
if t == settings["T_MAX_CALCULATION"]:
return coupon(t) + nominal_value(t)
return coupon(t) + nominal_value(t) + present_value(t+1) * (1/(1+i))**(1/12)
Description
Input
The runplan stores the information on the valuation date which is December 2022.
input.pyrunplan = Runplan(data=pd.DataFrame({
"version": [1],
"valuation_year": [2022],
"valuation_month": [12],
}))
Model point contains data on the attributes of the financial asset. The bond has a nominal value of €1000 and a coupon rate of 3%. The term of the bond is 120 months (10 years). It has been issued in June 2022.
input.pymain = ModelPointSet(data=pd.DataFrame({
"id": [1],
"nominal": [1000],
"coupon_rate": [0.03],
"term": [120],
"issue_year": [2022],
"issue_month": [6],
}))
The interest rate, that will be used for discounting, is constant and amounts to 2%.
input.pyassumption = dict()
assumption["INTEREST_RATE"] = 0.02
Model
End month
This variable represents the number of months between the valuation date and the end of the bond. The t_end variable will be used for the nominal value's formula.
model.py@variable()
def t_end():
years = main.get("term") // 12
months = main.get("term") - years * 12
end_year = main.get("issue_year") + years
end_month = main.get("issue_month") + months
if end_month > 12:
end_year += 1
end_month -= 12
valuation_year = runplan.get("valuation_year")
valuation_month = runplan.get("valuation_month")
return (end_year - valuation_year) * 12 + (end_month - valuation_month)
Calendar year and month
Calendar year start with valuation date. The valuation year and month are read from the runplan.
model.py@variable()
def cal_month(t):
if t == 0:
return runplan.get("valuation_month")
if cal_month(t-1) == 12:
return 1
else:
return cal_month(t-1) + 1
@variable()
def cal_year(t):
if t == 0:
return runplan.get("valuation_year")
if cal_month(t-1) == 12:
return cal_year(t-1) + 1
else:
return cal_year(t-1)
Coupon
Each year, the investor receives a coupon. It is calculated by multiplying the nominal value and the coupon rate.
model.py@variable()
def coupon(t):
if t != 0 and t <= t_end() and cal_month(t) == main.get("issue_month"):
return main.get("nominal") * main.get("coupon_rate")
return 0
Nominal value
At the end of the term, the investor receives back the nominal.
model.py@variable()
def nominal_value(t):
if t == t_end():
return main.get("nominal")
return 0
Present value
Cash flows are discounted with the interest rate read from assumptions to calculate the present value.
model.py@variable()
def present_value(t):
i = assumption["INTEREST_RATE"]
if t == settings["T_MAX_CALCULATION"]:
return coupon(t) + nominal_value(t)
return coupon(t) + nominal_value(t) + present_value(t+1) * (1/(1+i))**(1/12)
Results
<timestamp>_output.csv t cal_month t_end cal_year coupon nominal_value present_value
0 12 114 2022 0.0 0 1100.670155
1 1 114 2023 0.0 0 1102.488002
2 2 114 2023 0.0 0 1104.308850
3 3 114 2023 0.0 0 1106.132706
4 4 114 2023 0.0 0 1107.959574
5 5 114 2023 0.0 0 1109.789460
6 6 114 2023 30.0 0 1111.622367
7 7 114 2023 0.0 0 1083.408754
8 8 114 2023 0.0 0 1085.198092
9 9 114 2023 0.0 0 1086.990385
10 10 114 2023 0.0 0 1088.785638
11 11 114 2023 0.0 0 1090.583856
12 12 114 2023 0.0 0 1092.385044
13 1 114 2024 0.0 0 1094.189206
14 2 114 2024 0.0 0 1095.996349
15 3 114 2024 0.0 0 1097.806476
16 4 114 2024 0.0 0 1099.619593
17 5 114 2024 0.0 0 1101.435704
18 6 114 2024 30.0 0 1103.254814
19 7 114 2024 0.0 0 1075.027382
...
113 5 114 2032 0.0 0 1028.301676
114 6 114 2032 30.0 1000 1030.000000
Notes:
- coupon - coupon is paid each year. The bond has been issued 6 months before that valuation date so the first payment is in the sixth month of the projection.
- nominal_value - the investor receives back the nominal at the end of the term (t=114).
- present_value - present value at the beginning of the projection is higher than the nominal because the coupon rate is higher than the interest rate.
Thanks for reading the post! If you have any questions or would like to discuss something, please feel free to use discussions or issues sections of the github repository. You can also use the comment section below!