Actuarial optimization

In the world of actuarial science, we frequently encounter optimization problems. These challenges are most prevalent in the realm of pricing, where our goal is often to achieve a specific objective, such as expected profit. In this post, we will dive into a simple actuarial optimization problem and demonstrate how to solve it using two tools: Excel's Solver and Python.

List of content:

1. Scenario
2. Excel's Solver solution
3. Python solution

Scenario

Let's consider a 3-year term policy with a net premium of €100. We aim to find a profit margin that yields a present value of premiums equal to €3000, assuming a discount factor of 0.98.

Excel's Solver solution

In Excel's Solver, we would follow these steps:

1. Setting up the problem:

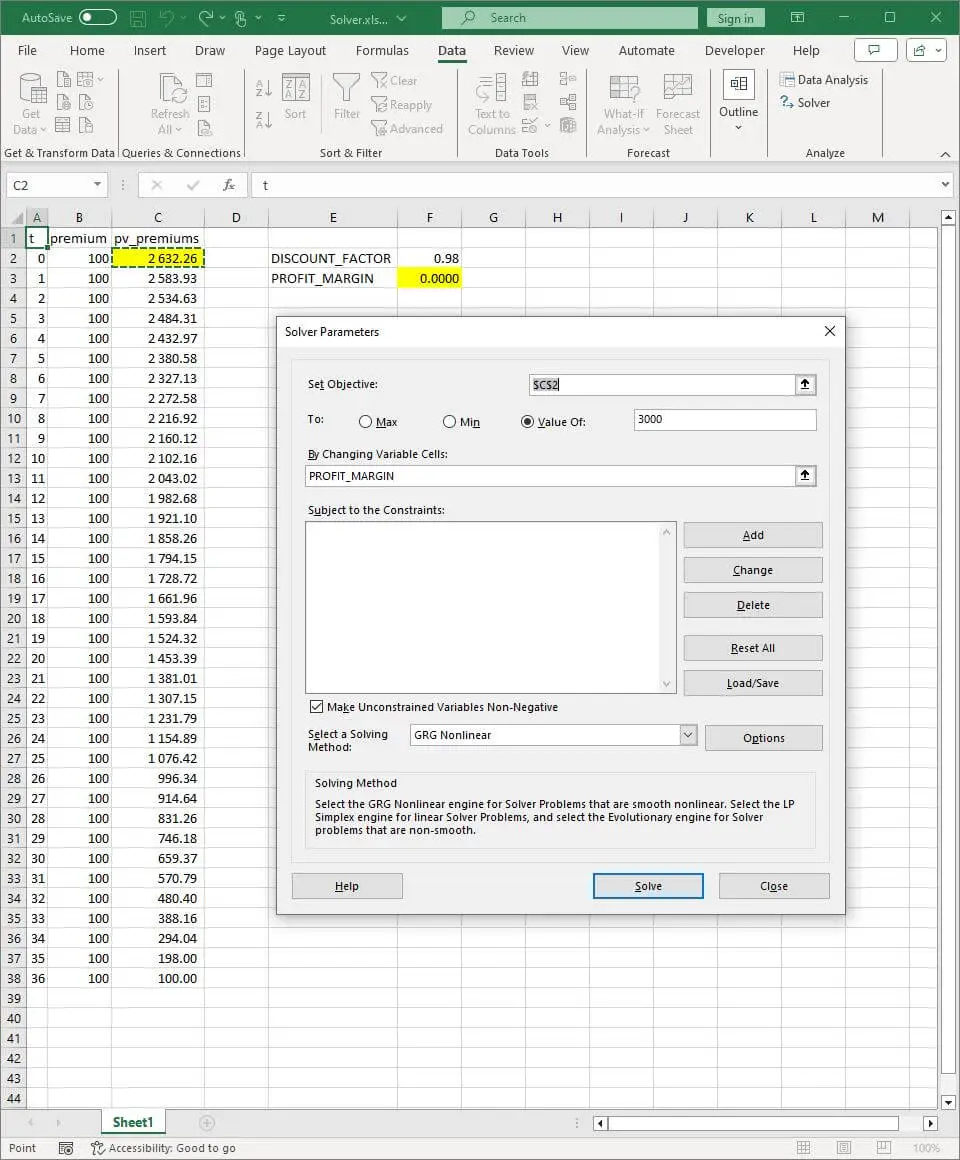
2. Solution found:

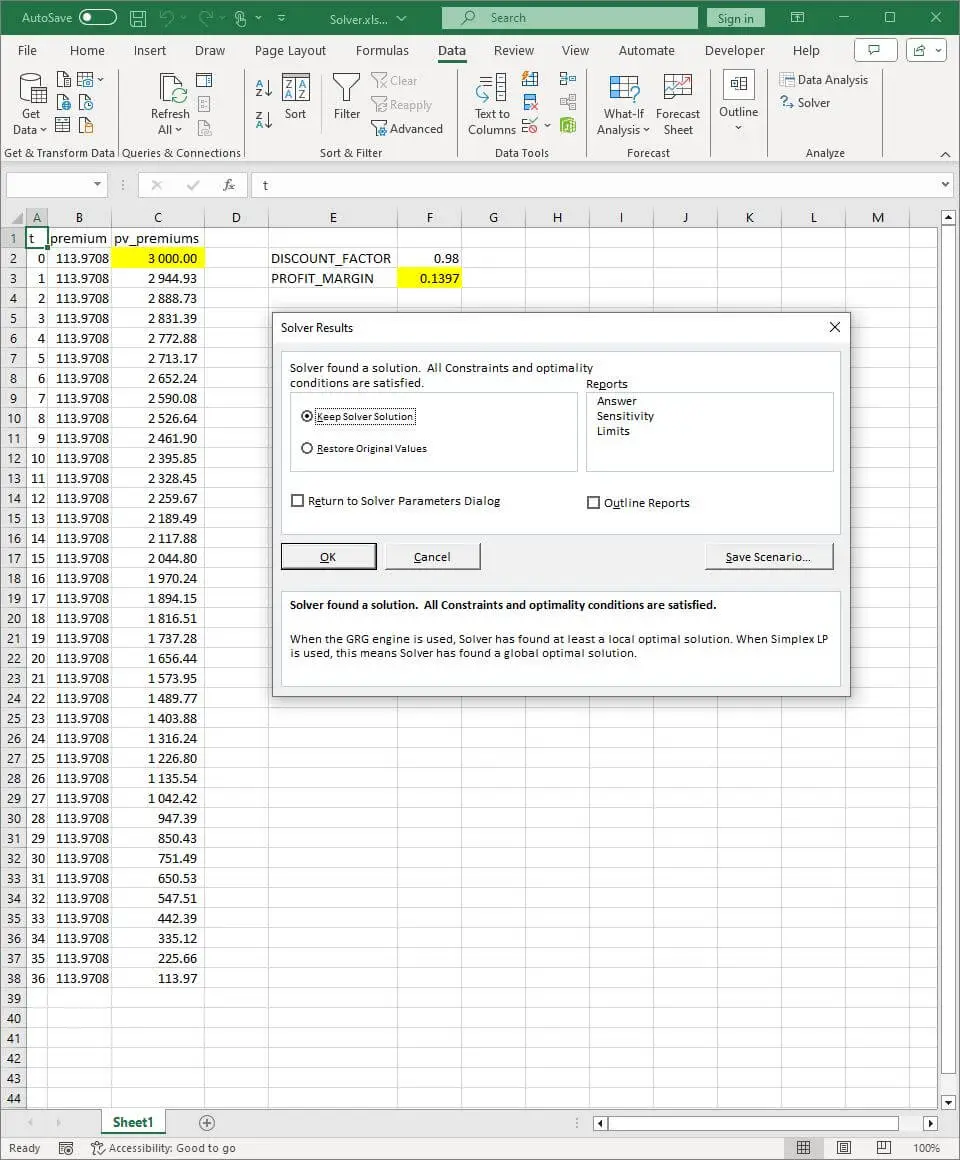
The profit margin that meets the criteria is 13.97%.

Python solution

In Python, we can achieve the same result using the scipy package. Here's the equivalent solution:

from scipy.optimize import root


DISCOUNT_FACTOR = 0.98


def premium(profit_margin):
    return 100 * (1 + profit_margin)


def pv_premium(t, profit_margin):
    if t == 36:
        return premium(profit_margin)
    return premium(profit_margin) + pv_premium(t+1, profit_margin) * DISCOUNT_FACTOR


def eqn(profit_margin):
    return pv_premium(0, profit_margin) - 3_000


myroot = root(eqn, 0)
print(myroot.x)  # Output: [0.13970692]

This Python code, which uses the scipy package, gives us the same answer as Excel. It calculates a profit margin of 13.97%.

Understanding the code:

Here's a simple explanation of the Python code:

• We set the discount factor to 0.98.
• The premium() function calculates the premium with the given profit margin.
• pv_premium() calculates the total premium over time, considering the discount.
• eqn() is the equation we want to solve.
• myroot helps us find the answer, which is the desired profit margin.

In this blog post, we looked at a common actuarial problem related to insurance pricing. We solved it using both Excel's Solver and Python with the scipy package. The consistent result of a 13.97% profit margin shows that actuarial tools can be powerful and versatile in today's data-driven world.